what do the sides of a parallelogram add up to
A quadrilateral whose ii pairs of sides are parallel to each and the four angles at the vertices are not equal to the correct angle, and then the quadrilateral is chosen a parallelogram. Besides, the opposite sides are equal in length.

Here,
Advertising = BC (opposite sides)
AB = CD (contrary sides)
Sum of all the four angles = 360 degrees
Learn more about the parallelogram here.
The of import properties of angles of a parallelogram are:
- If one bending of a parallelogram is a right angle, then all the angles are right angles
- Reverse angles of a parallelogram are equal (or coinciding)
- Consecutive angles are supplementary angles to each other (that ways they add up to 180 degrees)
Opposite Angles of a Parallelogram

In the above parallelogram, A, C and B, D are a pair of opposite angles.
Therefore, ∠A = ∠C and ∠B = ∠D
Also, we have dissimilar theorems based on the angles of a parallelogram. They are explained below along with proofs.
Opposite Angles of a Parallelogram are equal
Theorem: Prove that the contrary angles of a parallelogram are equal.
Given: Parallelogram ABCD.
To prove: ∠B = ∠D and ∠A =∠C
Proof:
In the parallelogram ABCD,
AB || CD and AD || BC
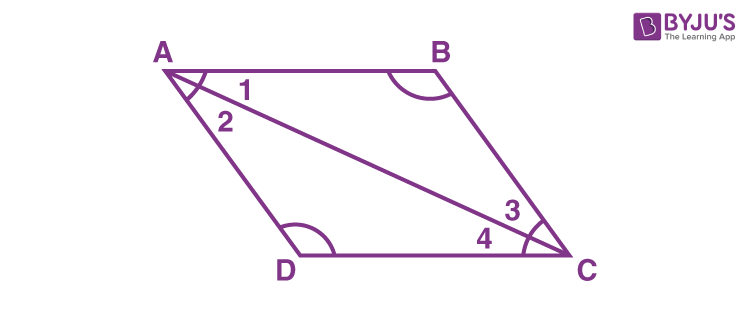
Consider triangle ABC and triangle ADC,
Air conditioning = Air-conditioning (common side)
We know that alternating interior angles are equal.
∠ane = ∠4
∠ii = ∠3
By ASA congruence criterion, two triangles are congruent to each other.
Therefore, ∠B = ∠D and ∠A =∠C
Hence, it is proved that the reverse angles of a parallelogram are equal.
Consecutive Angles of a Parallelogram
Theorem: Prove that any consecutive angles of a parallelogram are supplementary.
Given: Parallelogram ABCD.
To prove: ∠A + ∠B = 180 degrees, ∠C + ∠D = 180 degrees
Proof:

AB ∥ CD and AD is transversal .
We know that interior angles on the same side of a transversal are supplementary.
Therefore, ∠A + ∠D = 180°
Similarly, ∠B + ∠C = 180°, ∠C + ∠D = 180° and ∠A + ∠B = 180°.
Therefore, the sum of whatever two adjacent angles of a parallelogram is equal to 180°.
Hence, it is proved that any two adjacent or consecutive angles of a parallelogram are supplementary.
If one angle is a right bending, and so all iv angles are right angles:
From the above theorem, it can exist decided that if 1 angle of a parallelogram is a correct angle (that is equal to 90 degrees), and so all four angles are right angles. Hence, it will become a rectangle.
Since the adjacent sides are supplementary.
For example, ∠A, ∠B are next angles and ∠A = ninety°, then:
∠A + ∠B = 180°
90° + ∠B = 180°
∠B = 180° – ninety°
∠B = 90°
Similarly, ∠C = ∠D = 90°
Solved Examples
Example i:
In the adjoining effigy, ∠D = 85° and ∠B = (ten + 25)°, notice the value of 10.

Solution:
Given,
∠D = 85° and ∠B = (x + 25)°
We know that opposite angles of a parallelogram are congruent or equal.
Therefore,
(x + 25)° = 85°
ten = 85° – 25°
x = threescore°
Hence, the value of ten is 60.
Example 2: Detect the below figure.

Find the values of ten, y and z.
Solution:
From the given figure,
y = 112° {since the reverse angles of a parallelogram are equal)
z + 40° + 112° = 180° {the sum of consecutive angles is equal to 180°}
z = 180° – 112° – xl° = 28°
Also, x = 28° {x and x are alternating angles)
Therefore, 10 = 28°, y = 112° and z = 28°.
Example iii:
Two adjacent angles of a parallelogram are in the ratio 4 : 5. Observe their measures.
Solution:
Given,
The ratio of two adjacent angles of a parallelogram = 4 : 5
Let 4x and 5x the angles.
So, 4x + 5x = 180° {the sum of two adjacent angles of a parallelogram is supplementary}
9x = 180°
10 = 20°
Therefore, the angles are 4 × 20° = 80° and 5 × 20° = 100°.
Practice Issues
- Ii adjacent angles of a parallelogram are in the ratio 5 : 1. Find all the angles of the parallelogram.
- The contrary angles of a parallelogram are (3x – 4)° and (2x – one)°. Find the measures of all angles of the parallelogram.
- If one of the interior angles of a parallelogram is 100°, then find the measure out of all the remaining angles.
Source: https://byjus.com/maths/angles-of-a-parallelogram/
0 Response to "what do the sides of a parallelogram add up to"
Post a Comment